La tasa de descuento constituye un proxy del nivel de riesgo del proyecto y constituye la rentabilidad mínima que los accionistas esperan ganar dado el riesgo del mismo. Para que un proyecto genere valor debe superar dicha valla de rentabilidad la cual está estrechamente asociada al riesgo que los inversores perciben en el mismo. A mayor riesgo asumido, mayor será la rentabilidad exigida.
Si la tasa de descuento utilizada en la evaluación de un proyecto no es la tasa correcta la empresa puede terminar aceptando una inversión que debió ser rechazada o, también, descartar un proyecto que debió ser aceptado.
Aceptar un proyecto que debió rechazarse se produce por dos razones, una conceptual y otra matemática:
Razón conceptual: El proyecto fue aceptado porque el riesgo que se le atribuyó es menor del que representaba realmente. En términos gráficos, es como si la valla que debía superar el proyecto tuviera una menor altura que la correcta.
Razón matemática: Dado que la generación de valor se mide a través de las técnicas de valor presente y siendo la fórmula la siguiente:
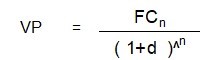
Se entiende que, si la tasa de descuento es menor que la adecuada, el denominador disminuye y la expresión total, el VP, aumenta. Una tasa de descuento que subestima el riesgo del proyecto sobreestima el flujo de caja a valores actuales:
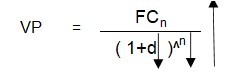
Flujos de caja sobreestimados pueden hacer que en vez que se rechace, el proyecto sea aceptado.
Las consecuencias de la situación opuesta, cuando la tasa de descuento sobreestima el riesgo del proyecto, son las contrarias. En términos gráficos, la valla tiene una altura mayor que la adecuada mientras que en términos matemáticos disminuye el VP de los FC lo que lleva a subestimar el VP de la corriente de efectivo del proyecto lo que, a su vez, podría llevar a rechazar un proyecto que realmente genera valor.
La determinación de la tasa de descuento es, pues, de vital importancia en la evaluación de las decisiones de inversión de cualquier agente económico. Muchas empresas emplean tasas de retorno contables o expectativas subjetivas de rentabilidad. Sin embargo; ninguna de las dos captura certeramente la rentabilidad esperada por los accionistas dado el nivel de riesgo asociado al proyecto.
La técnica más utilizada para determinar la tasa de descuento es la derivada del modelo de valoración de activos financieros o CAPM (Capital Asset Pricing Model).
La tasa de descuento de un proyecto se determina a través de la ecuación del CAPM:
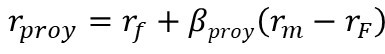
Es claro entonces que la tasa de descuento está en función de los parámetros de la ecuación (rf y rm -rf) y del β proy.
Antes de seguir es importante recalcar que el riesgo del proyecto es casi siempre diferente al riesgo de la empresa. Aun si el giro del negocio es el mismo, la forma de apalancar el proyecto puede llevar a que los riesgos entre ambos no sean equivalentes.
Para poder hallar el β proy se deben seguir los pasos siguientes:
Paso 1: Identificar a empresas o sector industrial comparable. Si el proyecto desarrollará la misma actividad de la empresa que lo ejecutará se utiliza el β de la compañía.
Los datos necesarios son: i) el βe (o β del equity también conocido como β apalancado), ii) el ratio de apalancamiento (D/E), ambos a precios de mercado y iii) la tasa de impuesto a la renta. Los tres elementos antes detallados pertenecen a los de las empresas o industria comparable.
Paso 2: Proceder a desapalancar el βe para lo cual se utiliza la ecuación Hamada:
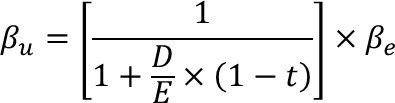
El βμ representa el riesgo de la empresa sin el efecto de la palanca financiera (y de ahí el término desapalancado). Visto desde otra perspectiva es el riesgo de la empresa si esta fuera financiada en su integridad por sus accionistas.
Cuando se tienen varias empresas comparables el βμ del sector es simplemente el promedio aritmético de las βμ individuales.
Paso 3: La βμ se vuelve apalancar, es decir se le incorpora el efecto de la estructura financiera del proyecto. Lo anterior se efectúa utilizando una forma modificada de la ecuación anterior:
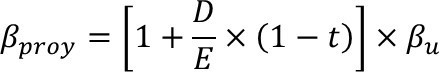
El D/E y la tasa de impuesto a la renta son las correspondientes al proyecto.
Para una mejor comprensión se presenta un cuadro que resume lo anterior:

Paso 4: El β proy es utilizado en la ecuación del CAPM para obtener el r proyecto (COK):
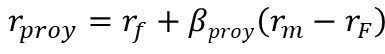
Es conveniente obtener, también el ru, esto es, la tasa de rentabilidad exigida por los accionistas asumiendo que el proyecto hubiera sido financiado en su integridad por los accionistas. La ecuación se modifica ligeramente:
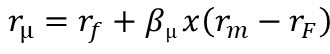
Los parámetros son los mismos, variando únicamente el β. Utilizándose ahora el βμ.
Paso 5: Se halla el WACC.
