La técnica más utilizada para determinar la tasa de descuento de un proyecto es la derivada del modelo de valoración de activos financieros o CAPM (Capital Asset Pricing Model).
La tasa de descuento de un proyecto se obtiene a través de esta ecuación:
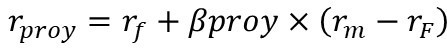
La tasa de descuento está, por lo tanto, en función de los parámetros de la ecuación (rf y rm -rf) y del β proy.
Los parámetros de la ecuación del CAPM (rf y rm -rf) conceptualmente se definen del modo siguiente:
· rf es la tasa libre de riesgo y se define como la tasa que paga hoy un activo libre de riesgo, en este caso un bono soberano.
· (rm -rf) es el diferencial entre lo que paga una inversión en el mercado (acciones) frente a lo que reditúa una inversión en un activo libre de riesgo. Se le conoce como “prima por riesgo de mercado”. Ese diferencial es la suma algebraica de los promedios geométricos de ambos componentes en el plazo más largo posible.
Dado que el modelo CAPM está pensado para mercados financieros líquidos, profundos y transparentes los datos (β y parámetros) para aplicar la ecuación del modelo están basados preferentemente en el mercado americano. Obtener a una tasa de descuento aplicable a nivel local implica incorporar a la ecuación el riesgo país.
Es importante tener en cuenta lo siguiente:
a) No se debe confundir el rf que constituye el elemento inicial de la ecuación con el rf de la prima por riesgo de mercado. Tal como se señaló anteriormente el primero es la tasa de rendimiento de un activo libre de riesgo en el momento de la evaluación en tanto que el otro es el promedio geométrico de la rentabilidad de un activo libro de riesgo en el mayor plazo posible.
b) La tasa del activo libre de riesgo, primer rf de la ecuación, es el correspondiente al rendimiento de dicho activo al plazo más cercano a la duración del proyecto. Sin embargo; algunos analistas utilizan el rendimiento al plazo más largo posible.
c) El promedio de ambos componentes en la prima por riesgo de mercado debe ser geométrico ya que los rendimientos ganados se van acumulando año tras año de manera similar a una tasa de interés compuesto.
d) El plazo de la prima por riesgo de mercado debe ser el más largo posible para poder “suavizar” la tendencia de los rendimientos percibidos a lo largo del tiempo.
e) El riesgo país que se suma a la tasa de descuento es el vigente el día de hoy.
No hay que perder de vista que la tasa de rentabilidad que entrega la ecuación es una tasa corriente, es decir ese rendimiento incorpora la inflación. Por lo tanto, las tasas de descuento halladas a través del modelo son aplicables únicamente a flujos de caja expresados en dólares corrientes.
Si el modelo de pronóstico del proyecto está en moneda local, la conversión de la tasa de rentabilidad a dicha moneda se efectúa de la manera siguiente:

Se debe enfatizar, nuevamente, que esa tasa es solo aplicable a proyecciones financieras efectuadas en moneda corriente.
A continuación, se presentan las fuentes en donde se pueden obtener los datos de los parámetros de la ecuación del CAPM y los β por sector industrial. Tal como se mencionó anteriormente dichos datos están referidos al mercado americano.
Tasa de rendimiento del activo libre de riesgo:
El enlace lleva a la página de la Reserva Federal (FED) que detalla el rendimiento (yield) de valores emitidos por el gobierno americano a diferentes plazos.
Como ya se indicó anteriormente el analista debe escoger el rendimiento del activo (bono del tesoro) al plazo más cercano a la vida del proyecto. Alternativamente, se puede considerar el rendimiento del bono con el plazo más largo posible (30 años).
Prima por riesgo de mercado:
http://pages.stern.nyu.edu/~adamodar/New_Home_Page/datafile/histretSP.html
La página a la que se accede mediante este enlace presenta las rentabilidades anuales obtenidas desde inicios de 1928 hasta el 2019 para tres clases de activos financieros: i) bonos del tesoro americanos, ii) inversión en la bolsa de valores americana (índice S&P500) y iii) letras del tesoro americano. Asimismo, se entrega el valor anual de una inversión de US$100 efectuada en 1928 en esos tres activos para cada uno de los años del período.
Para el cálculo de la prima por riesgo de mercado sólo interesan el rendimiento de los dos primeros activos. Lamentablemente, el cuadro no detalla el promedio de las rentabilidades; pero es fácil obtenerla si se siguen estos pasos:
Paso 1: Determinar el valor de la inversión inicial y final en el plazo más largo posible.
En el caso de la inversión en acciones:
Inicios de 1928: US$100
Finales 2019 : US$502,443.41
Paso 2: Hallar la rentabilidad acumulada en esos años.
Siguiendo el ejemplo anterior:
Rentabilidad acumulada 1928-2019 = (502,443.41/100) – 1 = 5,023.43%
Paso 3: Calcular el promedio geométrico correspondiente.
Continuando con el ejemplo:
Rentabilidad promedio 1928-2019 = (5,023.43%)ˆ(1/92) – 1 = 9.71%
En términos nominales una inversión en la bolsa americana ha rendido en promedio 9.71% anual en los último 92 años.
Similar procedimiento se utiliza para hallar la rentabilidad de un bono del tesoro americano.
Los resultados así obtenidos se suman algebraicamente y se obtiene la prima por riesgo de mercado.
Riesgo país:
http://www.ambito.com/economia/mercados/riesgo-pais/
El riesgo país esta expresado en puntos básicos (pb) o basic points (bp). Dado que 100 puntos básicos equivalen a un punto porcentual, la conversión a términos decimales implica dividirlos entre 10,000.
β sectoriales:
http://pages.stern.nyu.edu/~adamodar/New_Home_Page/datafile/Betas.html
El enlace lleva a un listado de β sectoriales en diversas industrias americanas. Se debe seleccionar el βμ de una actividad similar a la desarrollada por el proyecto.

Comments are closed.